Geometry Advancements
To simplify the drawing of multidimensional hypercube, take the established two dimensional projected cubes and draw them with hidden lines in three dimensions. Then, remove the hidden lines to have a much simpler representations. When this is done with cube it becomes a regular three dimensional closed box that could be sitting on your desk.
| 3-cube | 4-cube | 5-cube |
|
|
|
The following demonstrates the bridge between three dimensional n-cubes and two dimensional orthographic projected(B3, B4, B5) cubes found on Wikipedia. The orthographic projections are multidimensional hypercubes projected onto a plane (2D). They are accepted n-cube diagrams. The three dimensional n-cubes above three dimensions, are new.
3D N-Cubes from 2D Mathematical Geometric Diagrams
|
3D Solids
with hidden lines removed as posted on Wikipedia |
3D N-cube Frames
3D projections as posted on Wikipedia |
2D Projections
2D orthographic projections from Wikipedia |
| 3-cube, a closed box | 3-cube with hidden lines | B3 Coxeter plane element |
|
|
|
|
| 4-cube | 4-cube with hidden lines | B4 Coxeter plane graph |
|
|
|
|
| 5-cube | 5-cube with hidden lines | B5 Coxeter plane graph |
|
|
|
|
The B5 Coxeter plane graph was used on the cover of
Regular Polytopes.
Did anyone else notice? It's featured on page 244.
To gain acceptance for his geometry, Donald Coxeter had linked his geometry to conventional algebraic geometry. This was his breakthrough to get acceptance from the algebraic geometric mathematicians. I've gotten acceptance for my three dimensional cubes by geometric mathematicians by demonstrating the link from my diagrams to the Coxeter based geometric diagrams of which they are already familiar.
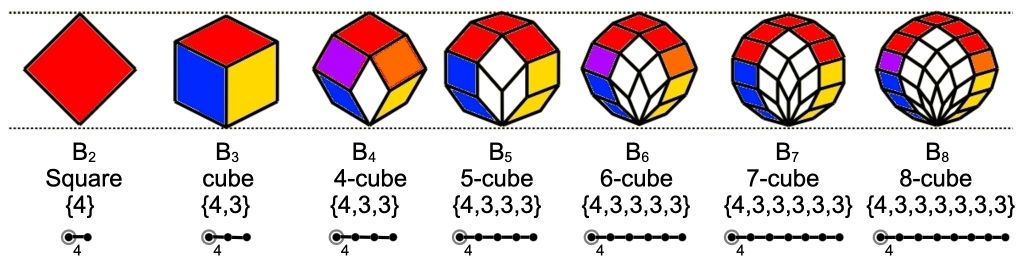
The following series of images are Coxeter elements, Coxeter groups: B2 to B8, redrawn as three dimensional solids. Think of the following images as hypercubes with opaque faces projected into three dimensions:
Geometry notes.
Multiverse geometry notes.
Multiverse science, my early notes.