Multiverse Geometry
and
Multi-Dimensional Geometry
This is my working document to create a Wikipedia Multiverse geometry article. Part of the work is an enhancement to the Lambda-CDM model, a model of our universe that it begins with a big bang and has cold dark matter(CDM) and dark energy.
"Multiverse geometry" Wikipedia search >> The page does not exist. You ... may create the page...
"Multi-dimensional geometry"
Wikipedia search >>
The page does not exist. You ... may create the page...
It is a Wikipedia Category
which has a lists of Wikipedia articles, including my
hidden line
article.
"Spacetime geometry" Wikipedia search >> Redirects to [[Spacetime]], topic: Curved manifolds. Above Curved manifolds is [[Riemannian geometry]] which is a [[Non Euclidean geometry]].
|
Geometry popularity list ordered by creation date.
Popularity measured by the amount of websites returning results. Euclidean geometry is the most popular and oldest geometry. Note, search counts change from time to time. | ||
| Search string (click Tools) | As of May 17, 2024 Google search >> | |
| "Multiverse geometry" | About 2,220 results. | |
| "Spacetime geometry" | About 141,000 results. | Uses non Euclidean geometry. |
| "Non Euclidean geometry" | About 808,000 results. | Variantes of Euclidean geometry. |
| "Analytic geometry" | About 3,820,000 results. | Analytic geometry is based on a coordinate system. |
| "Euclidean geometry" | About 4,180,000 results. | Based on straightedge, compass, and paper. |
Article topics
+ Overview introduction: generalized statements and definitions, and geometry of a universe: local and global.
+ Drawing Multi-dimensional Hypercubes. Working with 4D is interesting.
+ Geometric Dimensions, spatial and temporal
+ Are there objects with more than 3 spatial dimensions?
I was fascinated to know there is physical mathematical proof that there is only 3D spatial and one of time.
+ Using N-1 dimensions for demonstration. For example, 2D when explaining curved 3D.
+ Flatness in a 3 dimensional universe. This was interesting to learn.
+ Picturing curved space in our universe. Basic general relativity.
+ Our expanding universe
+ Bubble Universes
+ String theory Multiverse
+ Drawing Objects in a Multi-dimensional Universe
Proposed Wikipedia Page Content
(Section: Introduction and Overview)There is geometry for a single universe and geometry of multiple universes. Geometry of our universe includes [[Euclidean geometry]] where space is viewed as having straight lines, as in a [[Euclidean space]]. And [[non Euclidean geometry]] where space curves in the presents of mass, which is the geometry of [[spacetime]], [[spacetime geometry]] (Wikipeida spacetime topic: curved manifolds). In [[Laura Mersini-Houghton]] book, Before the Big Bang, she writes the phrase "curved spacetime geometries," in a footnote mentioning Einstein(general relativity), Minkowski(spacetime), and Riemann(mathematics), who are the fathers of curved 4 dimensional spacetime.
Euclidean geometry is useful for a global view of your universe as whole whether for our visible universe or beyond to infinity. Non Euclidean geometry is great for localized spatial representations such as the sun causing space to curve.
Constructive [[multi-dimensional geometry]] is useful for diagramming [[multiverse]] concepts such as many dimensional universes, and bubble universes within higher dimensions. Multi-dimensional [[constructive geometry]] uses techniques developed in 1, 2, and 3 dimensions. Methods derived in the first 3 dimensions are applied in higher dimensions. Multi-dimensional geometry includes drawing objects in higher dimensions using drawing techniques developed from drawing 1, 2, and 3 dimensional objects.
The method used to draw 4 dimensional hypercubes is derived from methods for drawing the lower dimensional shapes.

|
1 dimensional [[straight line]],
2D [[square]],
3D [[cube]],
|
Drawing Multi-dimensional Hypercubes
When working with curved spacetime and drawing representations of multiple universe, it helps to be able to draw multiple dimensional graph axes and to picture objects in multiple dimensions. This section is an exercise in working with n-dimensional space.
These are the base concepts to get started with drawing
[[hypercubes]]
in [[N-dimensional Euclidean space]]:
• Drawing [parallel lines]].
• Drawing [[without hidden line]]
• Using baselines as guidelines.
• Representing dimensions higher than 2, on a 2 dimensional computer screen or printed paper.
A line, square and cube are basic shapes.

|
To draw a square,
|
Dimensional baselines are lines to draw a square, cube, or hypercube upon. Or, draw axis of a [[Cartesian coordinate system]] where the baselines joined at the origin. The number of baselines is the number of dimensions in hypercube or the Cartesian coordinate graph.
To draw 3 dimensional baselines of a 3 dimensional cube,
squeeze the first 2 dimensional baselines to the left.
Add the 3rd baseline to the right.

| Given the 3 baselines, draw a 3 dimensional cube. | |

|
Use the baselines as guidelines to draw the other lines
|
To draw 4 dimensional baselines of a 4 dimensional hypercube,
squeeze the first dimensional baselines left.
Add the new dimensional baseline to the right.

| Given the 4 baselines, draw a 4 dimensional hypercube. | |

|
Having drawn the baselines,
|

|
Hare are diagrams of a [[tesseract]],
|
The above method of drawing baselines and hypercubes on top the baselines
works for as many dimensions as you choose.
If the cubes are drawn with the same height, as the number of dimensions increases,
the length of the edge lines will decrease.
Once the length of the edge line is less than a pixel,
the drawing would be a sphere on a computer screen.

A variation on constructive geometry, which is using a straightedge and compass with a pencil on paper,
is drawing with a program such as
[[LibreOffice]] Draw
on a computer.
When drawing, limit options to:
• Drawing a line which is drawing a line with a straightedge and pencil on paper.
• Copy & paste a line, then move the new line without changing the angle.
This is equivalent to drawing a parallel line to original line while maintaining the length of the line,
using a straightedge and compass with a pencil on paper.
• Select and rotate a line which maintains the line length.
Which is drawing a line with a straightedge and pencil on paper,
then using a compass to confirm the same length as the original line.

|
Square, cube, tesseract, and 5D hypercube built using wooden doweling and masking tape. |
Geometric Dimensions
There are two kinds of dimensions: spatial (bidirectional) and temporal (unidirectional). [Reference, [[Spacetime]]].
“Vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space,” from [[vector spaces]]. A dimension is a direction. A dimension requires one coordinate to specify the location of a point within the dimension. N dimensions have n independent directions. N dimensional space requires n coordinates to specify the location of a point within the dimensions.
3 dimensional directions are required to locate a point in our 3 spatial dimensions.
A temporal dimension which is a time dimension, is also required
to locate a point in our 3 spatial dimensions at a specified time.
An event has both location and time.
For example,
I was in the Canadian Rocky Mountains, Tooloulou's restaurant,
204 Caribou Street, Banff, Alberta, Canada,
September 10, 2023, at 8:00pm. local time.
Google Maps location longitude and latitude:
51.17671844860103 and -115.57156529508961.
An event has both location in our 3 spatial dimensions which can be given by longitude and latitude.
And a time dimension of a date, and time of day in a specific timezone.
(section in progress)
Using N-1 dimensions for demonstration
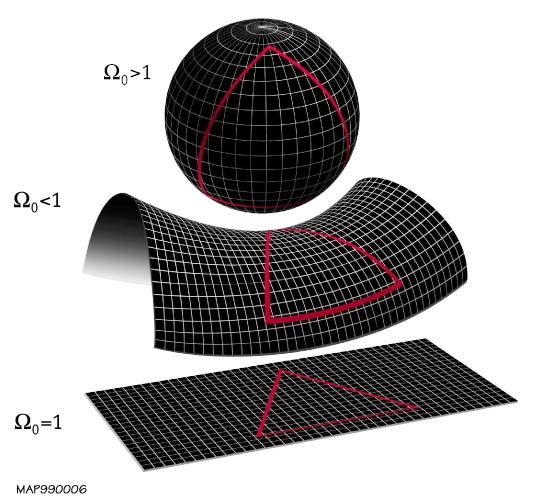
The page of [[Four-dimensional space]] geometry has space/dimensional analogy.A dimensional analogy is the study of how (n − 1) dimensions relate to n dimensions, and then inferring how n dimensions would relate to (n + 1) dimensions. It is a method to imagine 4 dimensions projected into our 3 spatial dimensions. Since we are 3 dimensional beings, to visualize 4 dimensional objects in our 3 spatial dimensions, we will use techniques from Flatland. The diagrams below shows the sphere, a 3D shape, above the 2D Flatland plane. It moves down into Flatland where it appears as a 2D circle on the Flatland 2D plane. The third diagram shows a sphere has moved below Flatland. As the sphere moves downward and through Flatland, it appears as circle of increasing size, and then the circle shrinks until it disappears as the sphere has gone below Flatland.

|
(x,y,z) sphere falling through (x,y) plane. |
The following N-1 dimension example uses the above diagram sequence.
Instead of sphere, the example uses a
4 dimensional [[hypersphere]].
A hypersphere, or n-sphere,
is the locus of points at equal distance (the radius) from a given center point.
A 1-sphere is a one dimensional circle on a 2 dimensional plane.
A 2-sphere is a two dimensional sphere in 3 dimensions.
A 3-sphere is a three dimensional sphere in 4 dimensions.
Given an (x,y,z,a)
4D [[hypersphere]]
where the dimensions of (x,y,z) are our 3 spatial dimensions.
And (a) is an added 4th spatial dimension.
n-1 for (x,y,z,a), would be:
(x,y,a) 3D sphere falling through (x,y) plane.
(x,z,a) sphere falling through (x,z) plane.
(y,z,a) sphere falling through (y,z) plane.
That's the total of a 4D hypersphere falling through our 3 spatial dimensional planes.
The hypersphere would appears as a point in each of the 3 planes.
As the hypersphere continues to move through our 3 dimensions,
it would be a circle in each of our 3 planes,
which is sphere in our 3 spatial dimensions.
The 3D sphere would increases in size, in our dimensions, to it's maximum size,
then shrinks until it disappears from our 3D space.
+ Edwin Abbott Abbott used dimensional analogy in his book Flatland.
+ Using n-1 dimensions when drawing graph diagrams.
+ Consider showing expansion of space using a (x,y) dimensional sphere. When expanded, enlarged, galaxy clusters are farther apart.
+ By applying dimensional analogy, one can infer that a four-dimensional being would be capable of similar feats in three-dimensions, as a three-dimensional being’s feats from two-dimensional being.
+ Projections: A useful application of dimensional analogy in visualizing higher dimensions is in projection. A projection is a way of representing an n-dimensional object in n − 1 dimensions. For instance, computer screens are two-dimensional, and all the photographs of three-dimensional people, places, and things are represented in two dimensions by projecting the objects onto a flat surface
Are there objects with more than 3 spatial dimensions?
In a space with more than three dimensions, there can be no traditional atoms and perhaps no stable structures. A space with less than three dimensions allows no gravitational force and may be too simple and barren to contain observers.
In 1917, [[Paul Ehrenfest]] showed that neither classical atoms nor planetary orbits can be stable in a space with more than 3 spatial dimensions. Tangherlini also showed that traditional quantum atoms cannot be stable in a space with more than 3 spatial dimensions. If there is only a single time dimension and more than three spatial dimensions, the orbit of a planet about its Sun cannot remain stable. [References, [[Spacetime]], [[Dimensions of spacetime]]]
In his article, Max states that when there are more than 3 dimensions, two-body problem no longer has a stable orbit solution. He goes on to show why there could only be one temporal time dimension with the 3 spatial dimensions. It's a strong argument that only 3+1-dimensional spacetimes are inhabitable by intelligent life. [Reference, On the dimensionality of spacetime (PDF), February 1997, by [[Max Tegmark]] (tegmark@mit.edu), Institute for Advanced Study, Princeton]

|
Max Tegmark's dimensional chart.
|
From a pragmatic point of view, as a 3D [[sphere]] would move through 2D space, a 4D [[hypersphere]] would move through 3D space: the sphere or hypersphere would appear as point in the lower dimensional space, grow from small to a maximum size, then shrink out existence in the lower dimensional space. Objects appearing and disappearing have not been observed and are not scientifically reproducible in our 3 dimensional universe. Not being scientifically observable does not confirm 4 dimensional objects do not exit, however it does support Ehrenfest's theory and Tegmark's argument that we do not live in a universe of objects greater that 3 dimensions, that we live in a 3 dimensional universe, a universe of 3 dimensional objects.
Flatness in a 3 dimensional universe
This is geometry on the global universe wide scale.
A sheet of paper laid on a table top lays flat. Draw a triangle on it and the sum of the inner angles is 180 degrees. Draw a triangle on beach ball and the sum of the inner angles is greater than 180 degrees. Using n-1 dimensions, given (x,y,z) Euclidean spatial dimensions: a triangle in (x,y) dimensions or (x,z) dimensions or (y,z) dimensions will have an inner angle sum of 180 degrees. In fact, any triangle having (x,y,z) coordinates in Euclidean space will have inner angles sum of 180 degrees.
Shape of the universe: One can experimentally do calculations to determine the curvature. From experimental calculations, within experimental error, the universe seems to be spatially flat. One method is to calculate geometric angles across the observable universe using the CMB. Using that method, it was determined that the sum of the angles is 180° within experimental error, again, showing the universe seems to be spatially flat.
In our (x,y,z) spatial dimensional universe, on a macro view, on a galactic view, research shows that triangles have an inner angle sum of 180 degrees with experimental acceptance. Therefore, our three-dimensional sheet of paper Euclidean space 3 space is flat.
Picturing curved space in our universe
This is geometry on the local scale. Around objects of large mass, triangles with have an inner angle sum greater than 180 degrees
Non-Euclidean geometry is used with the curvature of space.
Our expanding universe
Around objects of large mass, triangles with have an inner angle sum greater than 180 degrees
+ Expansion of space using a (x,y) dimensional sphere. When expanded, enlarged, galaxy clusters are farther apart.
+ What is the universe expanding into?
Not expanding into anything.
The non-gravitationally bound galaxies are moving away from each other.
The space between them is
expanding.
If the distance between galaxy culsters and the galaxy cluster we are in,
is given have a set of number, for example:
{c1,c2,c3,...}
then in an an expanding universe, the distance would increase:
{c1+d1,c1+d2,c3+d3,...} where d1,d2,d3 are positive numbers.
Note,
the sum of the numbers 1,2,3,..., is infinite.
the sum of the numbers 1,2,3,..., plus the sum of the distance: d1,d2,d3, is also infinite.
In an infinite universe, an expanding universe stays the same size, infinite,
but the distance between the galaxy clusters increases.
In Facebook, The James Webb Space Telescope (JWST) question,
"Spacetime is expanding we know. But expanding into what?"
My posted comment
was #778:
If the universe is infinite because it's
flat--astronomically speaking--the universe continues to expand into infinity.
Space can continue to grow and grow and grow, and still be the same size, infinite.
Drawing Bubble Universes
Multiverse universes are not literally bubble shaped universes. Bubble universe is a [[metaphor]]. If a person lives in a bubble, they are isolated, separated, from others around them. Two bubbles universes are independent of each other, separated.
Our visible universe could be considered as a bubble in that our visibility is spherical around us. Bubbles are spherical in shape.
Based on the CMB image, draw our visible universe as a bubble.
For example, show 2 [[Bubble Universes]] colliding to create the cold dark patch in the [[cosmic microwave background]] (CMB), as suggested by [[Laura Mersini-Houghton]].
Different bubbles may experience different spontaneous symmetry breaking, which results in different properties, such as different [[physical constants]] such as the [[gravitational constant]] G.
Links
Wired magazine,
How Universes Might Bubble Up and Collide.
Discovery,
What is the Multiverse?
PBS Nova,
Gravitational Waves From Bubble Universe Collisions? Theorists have suggested a new way to detect the existence of other universes.
Science Museum
London, UK, blog: The Science of the Multiverse, ...
Instead of being a single spherically symmetric expanding balloon-like structure,
our universe may look like a “multiverse”,
a cosmic froth of many different exponentially large bubbles (“universes”)
with different laws of physics operating in each one.
PBS Space Time,
How Many Universes Are There?
Neil deGrasse Tyson,
The Multiverse Hypothesis Explained
Neil deGrasse Tyson,
Why Quantum Physics Says There's a Multiverse
Brian Cox,
Infationary multiverse(short)
Brian Cox,
What Was There Before The Big Bang?
Universe Unveiled,
The Multiverse Theory: Are We Living in a Cosmic Bubble?
National Geographic,
Other Universes Finally Detectable? ... run-ins with other universes.
String theory Multiverse
String theory includes, brane-world scenario: physicists assume that the observable universe is a four-dimensional subspace of a higher dimensional space called the bulk. Brane: in string theory, a brane is a physical object that generalizes the notion of a zero-dimensional point particle, a one-dimensional string, or a two-dimensional membrane to higher-dimensional objects.

|
[[Brane cosmology]]
|
Drawing Objects in a Multi-dimensional Universe
Given a 3 dimensional object such as a ball with a stick stuck into it, a forth spatial dimensional stick, a four dimension being could swing it around and we would see a 3 dimensional ball moving around without anything causing it to move. 2 four dimensional objects could bump into each other where we would see a single 3 dimensional object changing course without seeing that it had bumped into something because the bumping would have happened in the fourth dimension. None of those are observed in our universe.
Since 3 dimensional spacetime is stable, there is a variation of multiverses where there are many universes of 3 dimensional spacetimes. There can be 3 dimensional objects in each of the 3 dimensional spacetime universes.
Here I demo 3 dimensional objects in 6 dimensional space and ask,
If 2 object from separate dimensions share a point in space, do they touch?
The 3 dimensional objects in each universe are casual in that they effect effect other gravitationally.
If there was no gravitational effect across the universes, there would be no causation across the universes.
Dimensional baselines are useful when constructing or drawing [[n-dimensional]] [[hypercubes]] and constructing n-dimensional coordinate axes. Multi-Dimensional axes are useful when creating higher dimensional [[Cartesian coordinate system]] objects(higher than 3 dimensions) for studies in [[physics]] and [[mathematics]] (I’ll need a reference for this statement).
vmu and dmu are universes. Our visible universe and a dark universe.
vmu has spatial dimension, (x,y,z).
dmu has spatial dimension, (a,b,c).
There are 3 dimensional objects in vmu.
Set of objects Ov = {v: v ∈ vmu}
There are 3 dimensional objects in dmu.
Set of objects Od = {d: d ∈ dmu}
The 2 universes make a multiverse = vmu ∪ dmu
= 3 dimensions space(x,y,z) + 3 dimensions of space(a,b,c)
= 6 dimensions of space(x,y,z,a,b,c)
A 3 universe multiverse would have
9 dimensions of space(x,y,z,a,b,c,d,e,f) and 1 dimension of time
for a total of 10 dimensions of multiverse spacetime.
There is one temporal time dimension in the multiverse.
Both universes share the same time dimension.
= 6 dimensions of space(x,y,z,a,b,c) + 1 dimension of time
= 7 dimension of spacetime
The multiverse uses the same [[Einstein field equations]](EFE) which are based on multi-dimensional Riemann math. If EFE works for 4(3D space + 1D time) dimension, then should work fine for 7 or 10 dimensions.
Reference Notes
Sample of referencing a book:
Paul Davies's book The Goldilocks Enigma (2006) reviews the current state...
Types of Geometry
The 2 major types are those that have drawings or non-coordinate graphs, and that which is geometry using coordinates and coordinates graphs.
[[Euclidean geometry]] is constructive geometry. Constructive geometry redirects to: [[Straightedge and compass construction]] geometry. Also known as ruler-and-compass construction or Euclidean construction. There are methods for creating things with no more than a compass and an unmarked straightedge. Euclidean geometry is more concrete than other systems such as set theory which can assert something’s existence with a method to create it within the system.
[[Non-Euclidean geometry]] ...
[[Synthetic geometry]] is geometry without the use of coordinates. It is sometimes referred to as axiomatic geometry or even pure geometry. It includes Euclidean geometry which is a mathematical system described in Euclid’s textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these, logically derived.
[[Projective geometry]]
...
In essence,
a projective geometry may be thought of as an extension of Euclidean geometry
in which the "direction" of each line is subsumed within the line as an extra "point",
and in which a "horizon" of directions corresponding to coplanar lines is regarded as a "line".
Thus, two parallel lines meet on a horizon line by virtue of their incorporating the same direction.
Idealized directions are referred to as points at infinity,
while idealized horizons are referred to as lines at infinity.
In mathematics,
the concept of a
[[projective space]]
originated from the visual effect of perspective,
where parallel lines seem to meet at infinity.
Axioms of projective space
Any given geometry may be deduced from an appropriate set of axioms.
Projective geometries are characterized by the "elliptic parallel" axiom,
that any two planes always meet in just one line, or in the plane;
any two lines always meet in just one point.
In other words,
there are no such things as parallel lines or planes in projective geometry.
Projective geometry later proved key to Paul Dirac's invention of quantum mechanics.
In more advanced work,
Dirac used extensive drawings in projective geometry to understand the intuitive meaning of his equations,
before writing up his work in an exclusively algebraic formalism.
[[Analytic geometry]]
is based on a coordinate system to express geometric properties by means of algebraic formulas, geometry into algebra. Examples, a line: y = 2x + 1, a circle: x2 + y2 = 7.
[[Cartesian space]]
was Euclidean in structure.
Britannica article under multidimensional space, mathematics: Arthur Cayley, British mathematician. Cayley was in Trinity College, Cambridge, in 1838-1846. In 1863 he accepted the Sadleirian professorship in mathematics at Cambridge.
In geometry Cayley concentrated his attention on analytic geometry, for which he naturally employed invariant theory. For example, he showed that the order of points formed by intersecting lines is always invariant, regardless of any spatial transformation. In 1859 Cayley outlined a notion of distance in projective geometry (a projective metric), and he was one of the first to realize that Euclidean geometry is a special case of projective geometry—an insight that reversed current thinking. Ten years later, Cayley’s projective metric provided a key for understanding the relationship between the various types of non-Euclidean geometries.
Albert Einstein's theory of general relativity is that physical space itself is not Euclidean. General relativity is based on a self-consistent non-Euclidean geometry.
Drawing Cubes and Spheres
For a [[cube]]:
+ Centered at the origin: (0,0,0),
+ With edges parallel to the axes and with an edge length of 2,
+ The [[Cartesian coordinates]]
of the vertices are
(±1, ±1, ±1)
while the interior consists of all points
(x0, x1, x2) with −1 < xi < 1 for all i.
Formally, a [[sphere]] is the set of points that are all at the same distance r from a given point in three-dimensional space. A sphere is hallow. A solid sphere is referred to as ball. Bubbles such as soap bubbles take a spherical shape in equilibrium.
From an Oxford University, Trinity College course:
ASO: Multidimensional Analysis and Geometry (2022-23)
Students will understand the concept of derivative in n dimensions...
Some set theory notation:
Subsets A ⊆ X with finite diameter, i.e. for which diam(A) = sup{d(a1, a2) a1, a2 ∈ A} < ∞
If A and B are subsets of X, define A + B = {a + b : a ∈ A, b ∈ B}
Search:
Multi-dimensional objects
Multi-dimensional geometry
n-dimensional space on Wikipedia is redirected to “Dimension”.
Dimension: In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it. A surface has a dimension of two (2D) because two coordinates are needed to specify a point on it. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.
There are 2 major sections: “In mathematics” and “In physics”.
The link: https://en.wikipedia.org/wiki/High-dimensional_space
redirects to Dimension/Additional dimensions which starts of, “In physics...” and includes: extra dimensions/hyperspace.
A Mathematician's Guided Tour Through Higher Dimensions
In 1884, Edwin Abbott wrote the popular satirical novel Flatland,
which used two-dimensional beings encountering a character from the third dimension
as an analogy to help readers comprehend the fourth dimension.
And in this era of “big data,” scientists, governments and
corporations build high-dimensional profiles of people, places and things.
Shape of the universe,
space:
One can experimentally do a calculation to determine the curvature.
From experimental calculations, within experimental error, the universe seems to be spatially flat.
In modern mathematics spaces are defined as sets with some added structure.
In physics, space is one of the few fundamental quantities in physics,
meaning that it cannot be defined via other quantities because nothing more fundamental is known at the present.
Today, our three-dimensional space is viewed as embedded in a four-dimensional spacetime,
called Minkowski space (see special relativity).
The idea behind spacetime is that time is hyperbolic-orthogonal to each of the three spatial dimensions.
Links
Nobel Prizes by university
[[Planck units]]

|

|
[[Solvay Conference]] 1927
|