Escher Geometric Shapes and Solids

This page is inspired by M.C. Escher's artwork based on geometry.

---

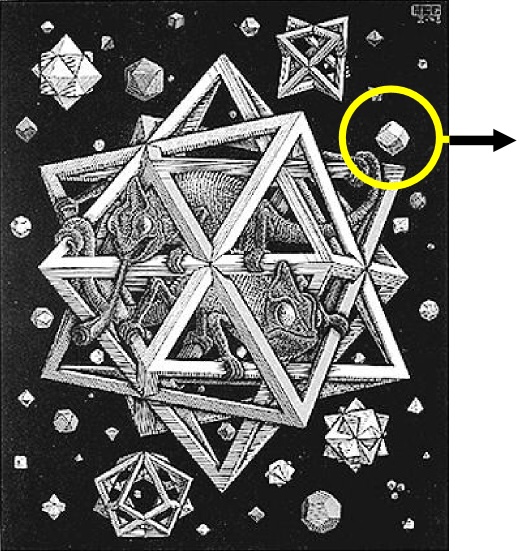
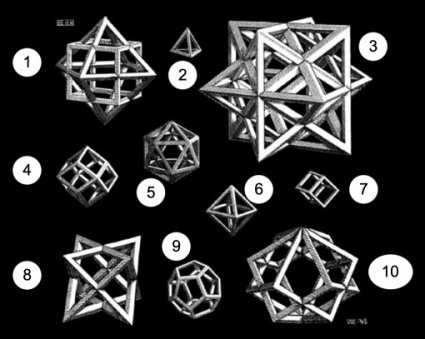
M.C. Escher's Study for Stars Shapes

Escher's Study for Stars (left) Escher's Stars (right)

The shapes are the frames of polyhedrons which are three-dimensional shapes with straight edges and sharp vertices, and flat faces that are polygons.

1. An octahedron compounded with a cube. It is a polyhedral stellation.
2. Tetrahedron, also known as a triangular pyramid.
3. Compound of three octahedrons or octahedron 3-compound or sometimes called Escher's solid.
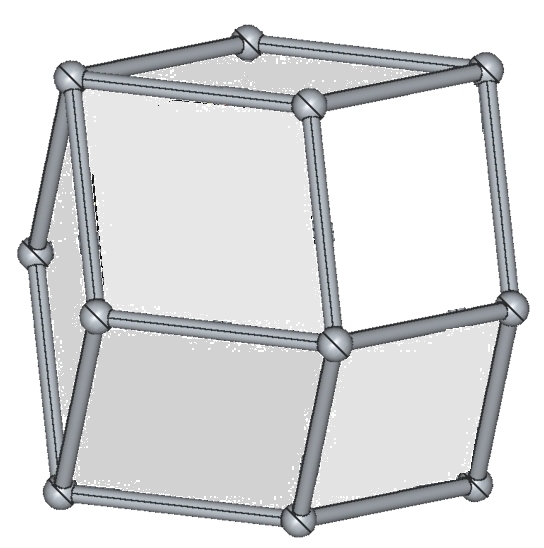
4. Rhombic dodecahedron which has 12 rhombus shaped faces.
   
5. Regular icosahedron a polyhedron with 20 faces that are regular triangles, equilaterals. Escher's sketch is similar to the one drawn by Leonardo da Vinci. There are 20 sided dice used in role-playing games like Dungeons & Dragons.
6. Octahedron, two pyramids matched at their square bases.
7. Cube
8. Stellated octahedron which is a compound of two tetrahedrons.
9. Regular dodecahedron which has twelve flat regular pentagon faces.
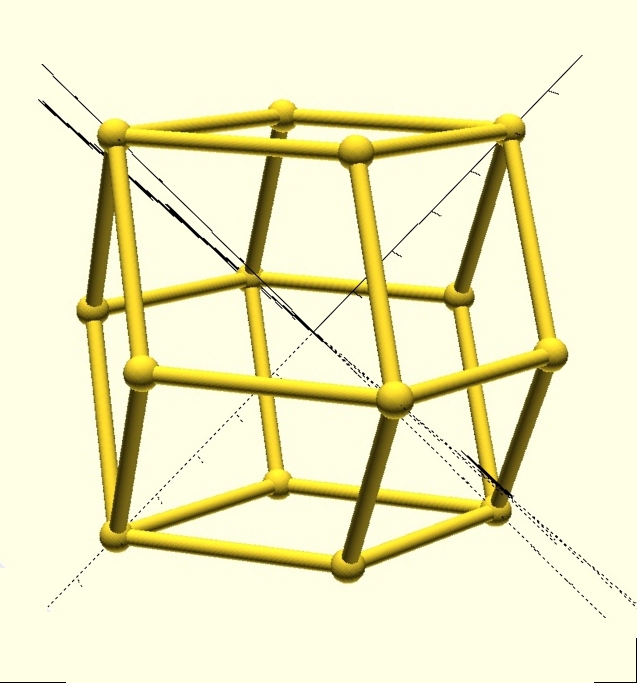
10. Two compound cubes. One rotated 45^o away from the other at two directions.

The base shapes are ancient. They include Plato's five Platonic solids: tetrahedron, cube, regular octahedron, dodecahedron, and icosahedron. Johannes Kepler also drew five Platonic solids in his book Harmonice Mundi.

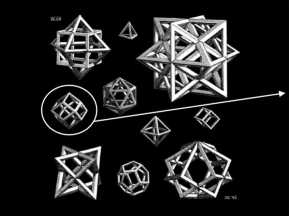
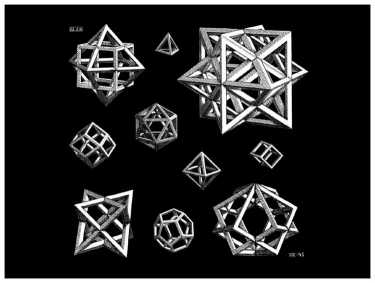
CAD Designs of Escher's Study for Stars Shapes
The designs are enhanced, Google Gemini generated designs from my initial OpenSCAD tesseract design.
Octahedron compounded in a cube. [3D STL Print file] [SCAD]	Tetrahedron, [3D STL Print file] [SCAD]	Compound of three octahedrons [3D STL Print file] [SCAD]
Rhombic dodecahedron, my CAD drawing. [3D STL Print file] [SCAD]	Regular icosahedron [3D STL Print file] [SCAD]	Octahedron [3D STL Print file] [SCAD]	Cube [3D STL Print file] [SCAD]
Stellated octahedron which is a compound of two tetrahedrons. [3D STL Print file] [SCAD]	Regular dodecahedron [3D STL Print file] [SCAD]	Two compound cubes. [3D STL Print file] [SCAD]

---

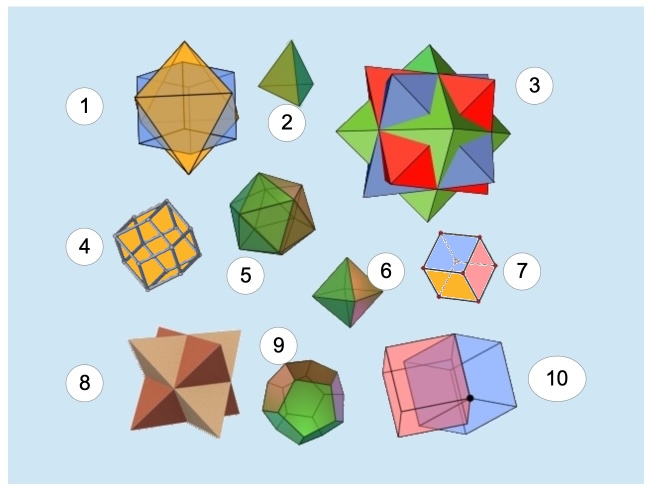
My version with freely available shapes

1. Octahedron compounded in a cube, generated from my prompting Gemini.
2. Tetrahedron, from Wikipedia.
3. Compound of three octahedrons from Wikipedia.
4. Rhombic dodecahedron, my CAD drawing.
5. Regular icosahedron from Wikipedia.
6. Octahedron, from Wikipedia.
7. Cube, my SVG image.
8. Stellated octahedron which is a compound of two tetrahedrons.
9. Regular dodecahedron from Wikipedia.
10. Two compound cubes. generated from my prompting Google Gemini.

---

4-Cube from Escher Art

Progression from art to CAD drawing:
1) Escher Stars	2) Cube extracted and rotated	3) CAD design with no hidden lines
1) Escher Study for Stars	2) Cube extracted and rotated	3) CAD design, no inner lines
1) Rhombic dodecahedron	2) CAD, Rhombic dodecahedron	3) CAD rotated(different CAD program)

---

Fair Use Escher Art